This whole thing started with a crashing path bug in 4.4.1 that I was looking at because 4.5 wasn’t giving me anything for this op. But then Stewart fixed 4.5 well enough to generate results. But then 4.5 has other problems. But the 4.5 problems are with output processing after slicing ok, and reported/acknowledged elsewhere. So this is several steps removed from what I had begun to write, and I’ve been lost a few times along the way. I’ll try to make it make sense anyhow.
This export includes four similar trace ops + one different:
trace-ends.kmz (139.2 KB)
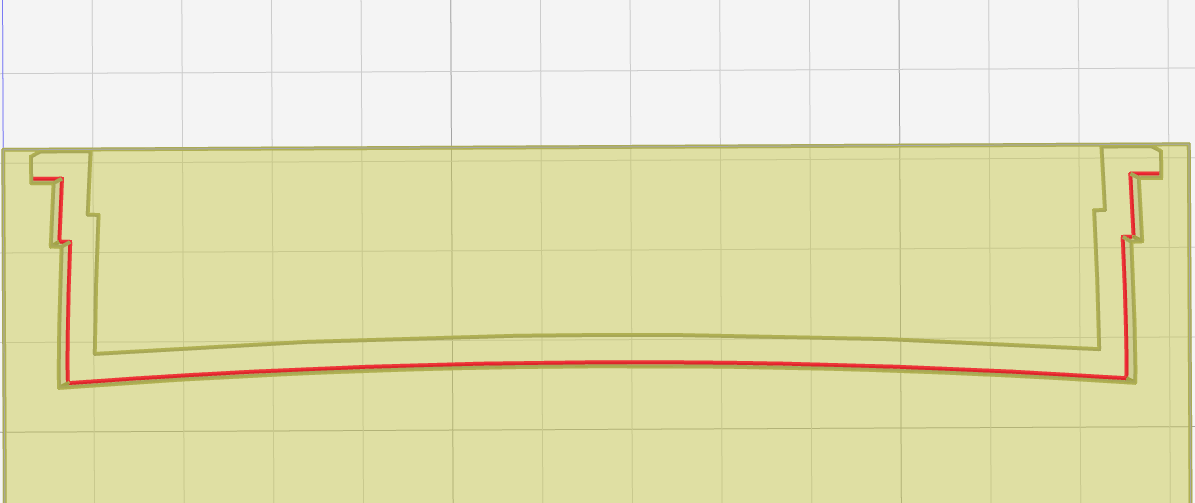
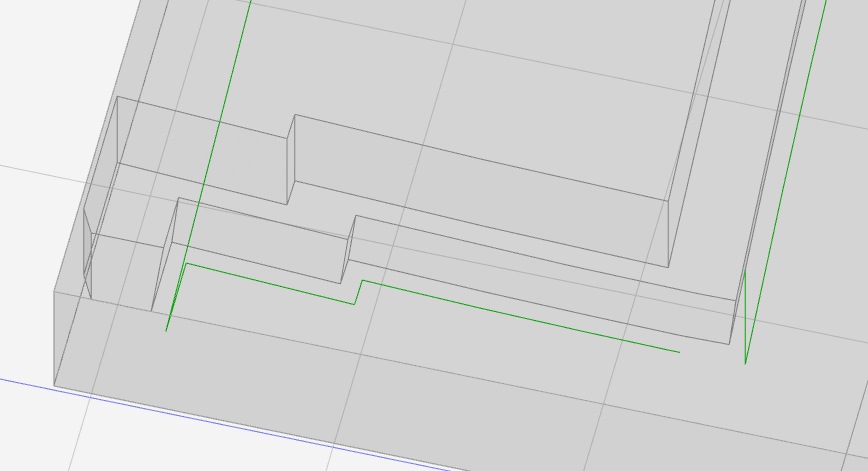
I want a path offset from this edge:
But the slicing result crashes into uncut material at the ends:
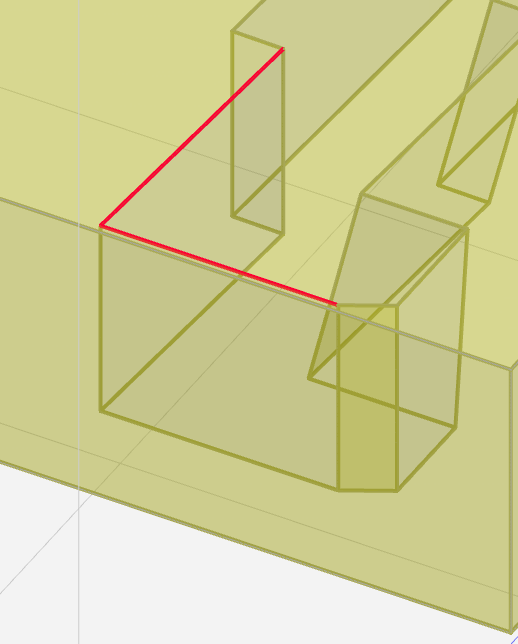
Here’s one end of the path I want:
The difference is the first is an “outside” offset and the second is an “inside” offset. The “outside” offset doesn’t work for an inside corner.
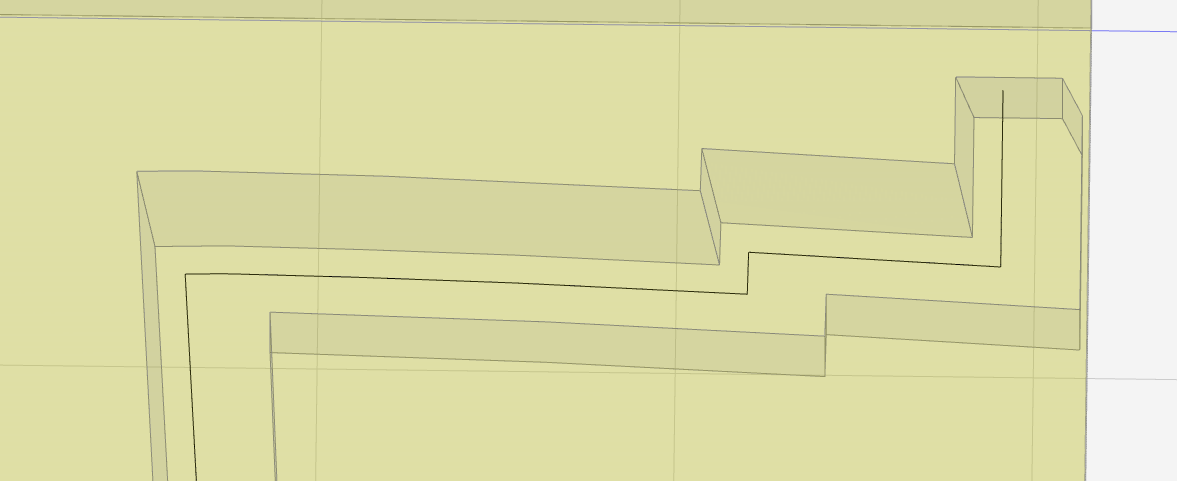
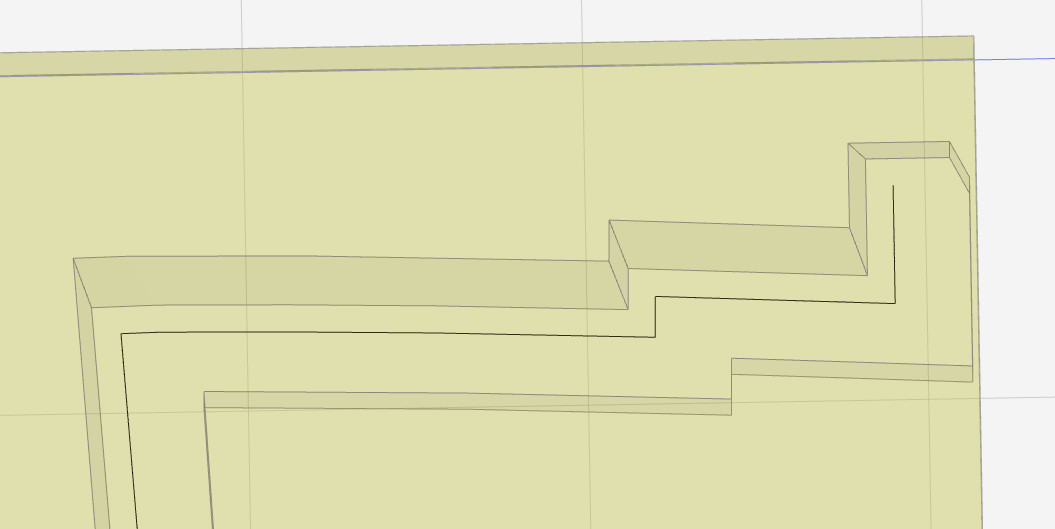
Flipping outside to inside was done by adding an extra segment at the other end of the path, which has the seemingly arbitrary effect of changing the inside/outside orientation of the open path:
The extra segment is harmless in this instance, but the option of adding segments until in-/out-sides flip may not be always available.
The inside/outside orientation matters because K:M, as far as I can tell, adds a tool radius to the ends of “outside” open paths and subtracts a radius from the ends of “inside” open paths. I can see that being a practically useful heuristic for paths that end at rightish-angle corners. Some thoughts about that:
- “outside” paths really don’t need to go any further than the end of the segment. I think.
- maybe the end of an offset segment is tricky to pin down – I’m thinking of the point where the offset is intersected by the source path’s normal at it’s end i.e. the center of a tool of radius equal to offset when it is tangent to the source path at its end point.
- “inside” paths ending at acute inside angles of uncut material need to be shortened by more than a radius. I haven’t thought of an easy answer. Maybe that’s just a limitation of the concept.
- maybe with hypothetical future modeling of uncut material … nope, I still haven’t thought of an easy answer.
- “inside” paths ending at obtuse inside angles of uncut material may be shortened by less than a radius.
- So the “inside”/”outside” distinction matters for open paths, but the labels are arbitrary for an open path. I think the Onshape way would be to assign an arbitrary[1] orientation and offer a click-to-flip control
- for open paths, the distinction matters for treatment of endpoints – but endpoint treatment is not well defined apart from the -radius heuristic
- “none” not-offset paths still may need to stop short in some cases, like short by a radius if meeting a perpendicular surface
- Open & closed paths are different animals
- “inside” end shortening can be needed, or not, on either side of an open path, so in addition to choosing in/out offset (end treatment) also need to choose which sides are in & out
- maybe separately for each end
So, some ideas:
- The selection UI could show an explicit distinction between open & closed paths – like change color on detecting path closure – to cue the user to different semantics & behavior, whatever that may be
- But instead of that, how about:
- How hard/laggy would it be to show offset paths in the selection UI (e.g. translucent, desaturated, thin, other distinction)? If not too bad:
- avoid the “inside”/”outside” concept entirely by showing (without word labels) where offsets would fall, and providing a “flip” widget. That seems to be the Onshape way.
- per-object overrides could get all targets for the intent of an op flipped the intended way in one op, but maybe more sane to say that it might take two ops to get all of multiple objects
- instead of trying to solve when and how much to shorten the ends of an open path, how about allow selection of edges or surfaces that the tool cutting the trace path can’t break (or ride over if co-planar with path)? Maybe different click-flavor and different selected color in the selection view.
- the first example being the “other” wall of an inside corner – instead of expecting K:M to always get that right automagically.
- other features near but not intersecting the trace path could be protected – or not – without expecting K:M to always get that right automagically.
[1]prolly deterministic but not obviously predictable
===========
other unexpected things
- thing1/2
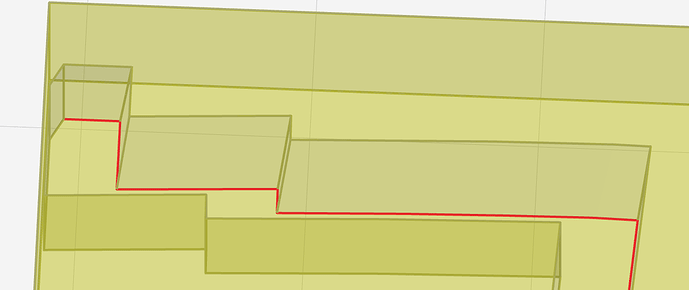
Either of the two paths above can be flipped to the opposite offset. That’s not useful, but an unexpected result might be worth a look.
In preview, all these offset paths have the extra segment across the top of the part (left in pic) which we’ve already discussed. The offset paths also have the break in the lower-right part of the pic. Because that’s closest to origin, I suppose. I’ve assumed that’s because the extra segment makes a closed loop which has to have a start/end break somewhere, so I’ve assumed that’s basically correct function.
The extra segment that closes the path happens after slicing, so the nominal “inside” and “outside” of the paths closed by the extra segment don’t relate to the inside or outside of the loop. Purely a side-effect of the extra segment bug, I assume.
For the ‘preview’ output loops that are offset inward from the trace path, the start/end gap looks like a radius distance (not shown). I assume that’s normal for output of a loop path. (although I think there’s an argument to be made for returning to the start point or having the option to do so)
For the ‘preview’ output loops that are offset outward from the trace path, like the example above, the gap is much larger. That doesn’t look like normal output. Evidence of something else awry?
- thing 2/2
The “none” offset result for this path on the top of the part:
appears at the bottom of stock: